Read the handout ``Finite Markov Chains.''
![]()
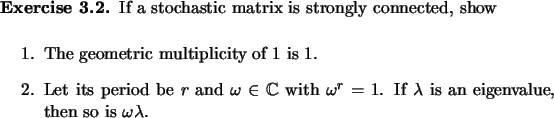
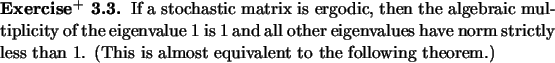
![]()
![]()
One way to guarantee that ![]() is doubly stochastic is to ask
is doubly stochastic is to ask ![]() .
A walk on a Cayley graph is always doubly stochastic. Having the generating
set
.
A walk on a Cayley graph is always doubly stochastic. Having the generating
set ![]() be closed under inverses makes
be closed under inverses makes ![]() , but we do that only to
invoke the Laundau-Odlyzko theorem.
, but we do that only to
invoke the Laundau-Odlyzko theorem.
The eigenvalue gap tells us about the rate of convergence to the
stationary distribution. This is always true, but easier if ![]() is
symmetric. Then the spectral theorem gives us an orthonormal basis
is
symmetric. Then the spectral theorem gives us an orthonormal basis
![]() , with
, with
![]() .
for
.
for ![]() . We can choose
. We can choose
![]() .
Then for
.
Then for ![]() the rotation that sends
those eigenvectors
to
the standard basis,
the rotation that sends
those eigenvectors
to
the standard basis,
![]() is diagonal, with entries its eigenvalues.
This ``separation of coordinates'' makes raising the matrix to
powers easy:
is diagonal, with entries its eigenvalues.
This ``separation of coordinates'' makes raising the matrix to
powers easy:
![]() , a diagonal matrix with
entries
, a diagonal matrix with
entries
![]() . This exponentially decays to the diagonal
matrix with entries
. This exponentially decays to the diagonal
matrix with entries
![]() . Conjugating by the inverse
of
. Conjugating by the inverse
of ![]() then gives
then gives ![]() .
.
To measure convergence of ![]() to
to ![]() , we need a measure of the
size of a matrix and apply it to
, we need a measure of the
size of a matrix and apply it to
![]() , which conjugated
by
, which conjugated
by ![]() gives a diagonal matrix with entries
gives a diagonal matrix with entries
![]() .
.
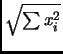 .
The Frobenius norm
.
The Frobenius norm 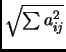 .
.
![]()
![]()
![]()
Thus
![]() . So for
. So for
![]() it
suffices to have
it
suffices to have
![]() .
.
Now we need to relate this bound on the operator norm to what we care
about: the deviation of the distribution from uniform,
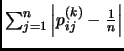 .
.
Set
![]() and
and
![]() .
If
.
If
![]() ,
then
,
then
![]() , so for all
, so for all ![]() and
and ![]() ,
,
![]() . So to be within
. So to be within ![]() of a uniform
distribution, we need
of a uniform
distribution, we need
![]() , which we
can achieve with
, which we
can achieve with
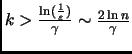 (since
(since ![]() is a constant)
and by
Landau-Odlyzko,
is a constant)
and by
Landau-Odlyzko,
![]() (
(![]() ,
,
![]() ,
, ![]() ), so we can let
), so we can let ![]() be
be
![]() , which leads to a similar diamater and we have proved
, which leads to a similar diamater and we have proved
![]()